GRAVITY
BASIC OBSERVATIONS
If you are holding a ball and let go of it, the ball falls down to the ground.
Alternatively, if you were to toss the ball up into the air, it goes up, slows down, stops, then falls back down.
This observation, of course, probably seems very obvious and banal. After all, it’s been a constant for the vast majority of human experiences. We often don’t stop to think how strange this phenomenon actually is. Some invisible force is yanking things in the air down to the ground? Why down? Why not up? Or sideways? Or, really, why at all?
It’s easy in the 21st century to say it’s because of gravity and call it a day. Well, for a lot of people anyway. Gravity is no mere afterthought. Its influence is everywhere, from our own planet to the vast expanse of the cosmos, moving the very heavens above us and giving form to the countless worlds within them. Something so fundamental to our reality begs to be understood. With that in mind, let’s take a closer look at all the ways gravity manifests, big and small, near and far.
ANCIENT THEORIES
Hundreds to thousands of years ago, long before the establishment of modern scientific methodologies, the study of the nature of reality and physics was considered a philosophical endeavor. Thus, people who spent their days considering questions about falling objects and cosmic curiosities were called natural philosophers.
Greek philosophers had various theories about the nature of gravity. Aristotle tied gravity to the four classical elements (earth, air, fire, and water) of which each had a natural place in the universe. Earth was thought as the heaviest element and thus had a natural tendency to move downward. Water was less heavy and remained over earth. Air was lighter and floated over the earth and water. Fire was the lightest element and was always reaching upward. It was also believed that heavier objects fell faster than lighter ones (which Galileo later disproved experimentally). Archimedes, on the other hand, explored the principles of buoyancy and displacement in which an object emersed in liquid would be forced upward at a rate equal to the weight of the liquid being displaced by the object. He saw buoyancy and gravity as two competing forces.
In ancient Chinese philosophy, there was an understanding that Heaven and Earth were interconnected. Inspired by the concept of Yin and Yang, representing a balance between opposing but complementary forces, it was proposed that the forces of Earth (Yin) and Heaven (Yang) influenced the movement and attraction of objects. Things like falling rocks had yin-like motion while rising smoke and flames had yang-like motion. Zou Yan also favored the idea of classical elements influencing the behavior of objects, though he proposed five (wood, fire, earth, metal, and water).
These ideas, like many other explanations of their time, relied on intuition and the application of broad, holistic concepts about the world. They were ultimately abandoned during the Scientific Revolution which saw a broad shift towards quantitative approaches to investigation in which empirical measurement and systematic experimentation were favored.
MASS
To understand a modern conception of gravity, first we must understand mass.
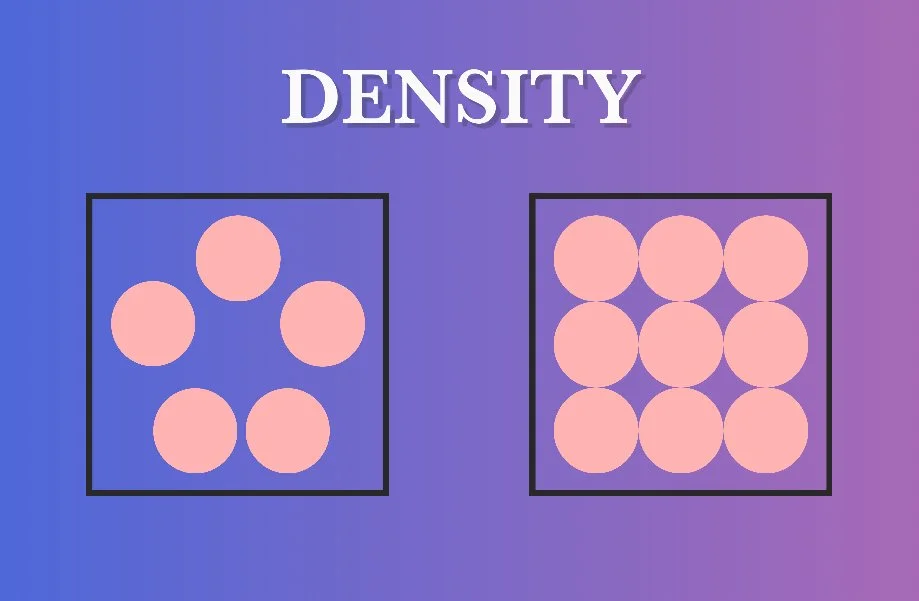
What is mass? Simply, mass is how much stuff makes up an object. If an object has more mass, then it is said to be more massive than an object that has less mass. This is distinct from an object’s size which is how much space the object’s mass takes up. If an object takes up more space, it is said to be bigger or larger than an object that takes up less space. If conditions allow for it, an object can potentially have any amount of mass combined with any size.
When you compare an object’s size to its mass, you are talking about density. If two objects are the same size but one object has more mass, it has higher density. Also, if two objects are the same mass but one object is smaller, it too has higher density. In fact, an object can be smaller than another object but still be much denser or be larger than another object but still be much less dense.
These distinctions are important when considering how gravity manifests for reasons that will become clear soon enough. In the meantime, you must know this one simple thing:
Everything that has mass, exerts gravity.
NEWTON’S LAW OF UNIVERSAL GRAVITATION
In what was possibly one of the most genius ideas ever thought of by a human being, late-17th century English physicist Isaac Newton determined that the Moon’s orbit around the Earth is governed by the same force that makes apples fall from trees.
By Newton’s time, Johannes Kepler’s laws of planetary motion were quite well-known. Newton believed that these motions of planets around the Sun could be explained by some kind of force acting between them. As early as 1666, Newton had developed a framework that unified Kepler’s laws with his own laws of motion to develop a theory of gravity.
Published in his most famous work in 1687, “Mathematical Principles of Natural Philosophy,” Newton described his law of universal gravitation which states:
“Any two bodies are attracted by a force proportional to the product of their masses and inversely proportional to their separation squared.”
This is expressed by the mathematical formula:
F = G * (m1 * m2 / r ² )
F is the force of gravity.
G is the gravitational constant.
m1 is the mass of the first object.
m2 is the mass of the second object.
r is the distance between the two objects.
The gravitational constant represents the intrinsic strength of gravity. This number is extremely small, which is why gravity is considered the weakest of the fundamental forces and why we don’t perceive everyday objects as having gravity (but they most certainly do). Newton himself did not learn the specific value of the gravitational constant. It was Henry Cavendish who successfully measured it in 1798 through his famous Cavendish experiment involving lead spheres and a torsion balance.
Every object with mass exerts a gravitational pull on every other object with mass, regardless of size or distance. The Sun has gravity. Earth has gravity. Even a grain of sand has gravity. In Newton’s law of gravitation, m1 and m2 represent the masses of the two interacting objects. Each mass contributes directly to the strength of the gravitational attraction between them, which is why they appear multiplied together in the equation. If either object’s mass increases, the gravitational force between the two objects increases by the same proportion. Gravity is therefore a mutual interaction: both objects pull on each other, and the force each experiences is equal in magnitude and opposite in direction, in accordance with Newton’s third law of motion.
Although the gravitational force between two objects is equal for both, equal force does not result in equal motion. How much an object accelerates in response to a force depends on its inertia, which increases with mass (as described by Newton’s second law of motion). For example, when a pencil falls toward the Earth, the Earth is also being pulled toward the pencil with the same gravitational force. However, because the Earth has vastly more mass, it accelerates by an immeasurably small amount, while the pencil accelerates rapidly. This difference in inertia is why objects of different masses fall at the same rate in a gravitational field: more massive objects experience more gravitational force, but they also resist acceleration by the same factor, causing the effects to cancel out.
Gravitational attraction acts toward an object’s center of mass. The center of mass is determined by how the object’s mass is distributed, and for an object with a roughly even distribution, such as a sphere, it lies at the geometric center. In sufficiently massive objects, gravity pulls material inward from all directions toward this center of mass. Over time, this inward pull causes the object to assume a spherical shape, since a sphere is the configuration in which gravity acts equally in all directions. This is why large bodies such as planets and stars naturally become spherical, while smaller objects lack sufficient gravity to overcome their structural strength and maintain irregular shapes.
As objects become more distant, the force of gravity between them becomes weaker via the inverse square law. If you double the distance between objects, the gravitational effect becomes 2 x 2 = 4 times weaker (or 1/4 its initial strength). If you make them 10 times more distant, the gravitational effect becomes 10 x 10 = 100 times weaker (or 1/100 its initial strength). Note: This is exactly how light diminishes with distance as well.
To reiterate, the distance between the objects is measured between their centers of mass, not their surfaces. This is very important when dealing with two objects of different sizes.
WEIGHT
When standing on a massive object, like a planet, its gravity continues to exert a force pulling you towards the object’s center of mass. However, the object’s own surface gets in the way and pushes back on you (this is called the normal force). The force of gravity on your body against the normal force of the ground is what creates weight.
Weight is calculated as:
weight = mass x gravity
If you reduce the gravity, then you’ll reduce the weight. The same person will weigh less on Mars than they will on Earth. But, wait… Mars only has about 10% of Earth’s mass but almost 40% of Earth’s gravity. Shouldn’t Mars only have 10% of the gravity?
It’s not only the mass that’s different between them. It’s their size. The radius of Earth, aka the distance from surface to center, is 6,370km while the radius of Mars is only 3,390km. This makes Mars about half the width of Earth. Despite only having 10% of the mass on Mars, you are about 3,000km closer to its center from the surface. According to the inverse square law, half the distance means four times the gravity. This is how you go from 10% of the gravity to 40%.
ORBITAL MECHANICS
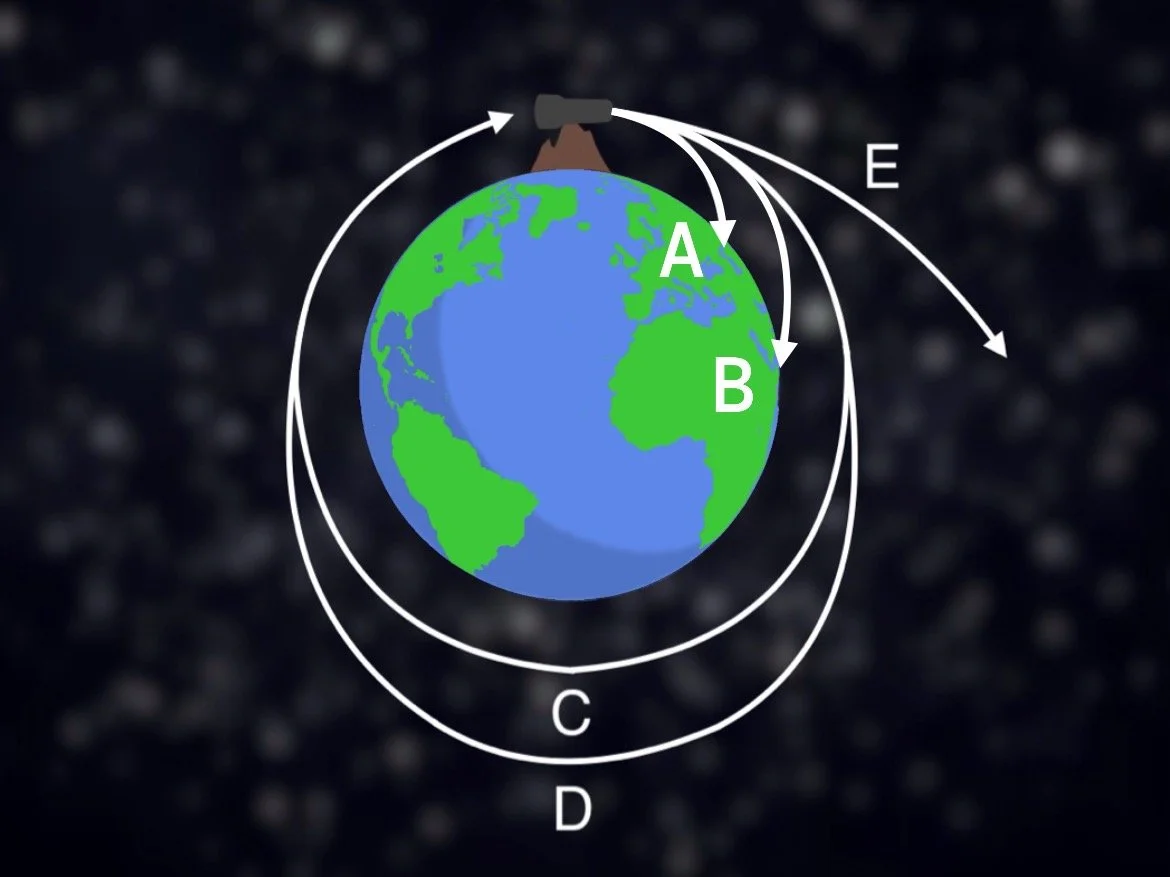
Newton didn’t stop there. This next part will really show how brilliant Newton’s mind was. As he continued to develop his laws of motion and study celestial mechanics, Newton formulated his ingenious cannonball thought experiment. It goes like this:
Imagine a cannon atop a mountain on Earth. You fire a cannonball which goes sideways but quickly drops to the ground (A). Earth’s gravity pulls the cannonball down. Now imagine we fire the cannonball faster. It would no doubt go sideways and get even further this time before again being pulled to the ground by Earth’s gravity (B).
But what if we fire the cannonball so fast that the rate at which it falls equals the rate at which the Earth curves away from it? You get what’s called an orbit (C). You are essentially constantly falling towards the planet but always missing it. This is what the Moon is doing around the Earth and what the Earth and all other planets are doing around the Sun.
As we know, gravity weakens with distance. Therefore, the speed at which a moon or planet must move around its parent object to maintain its orbit gets slower with distance. If you look at all the planets in our solar system, you will see that their orbital periods (the time it takes to do a full revolution around the Sun) get exponentially longer the further out they are. Mercury zips around the Sun in only 88 days but it takes Neptune 165 years to do the same. For the International Space Station to maintain its 400 km high orbit above Earth’s surface, it must move 27,600 km/h (17,000 mph), which gets it around the whole planet in just 90 minutes, or else it will lose altitude.
Back to our cannonball. You can also take this further by continuing to raise the speed. The cannonball will still be in orbit, but its orbit around the Earth will become more elliptical (D). In reality, all planetary orbits are elliptical to some degree, with a gradually shifting distance from the Sun. As is with Johannes Kepler’s second law of planetary motion, this elliptical orbit also changes the planet’s speed. The planet moves faster when it is closer to the Sun and slower when it is further.
Continue to fire the cannonball faster and faster and its elliptical orbit will get more and more extreme until it eventually reaches a threshold. Known as the escape velocity, the cannonball reaches a speed that allows it to completely overcome and break free of the planet’s gravity (E). The speed one must achieve to do this will vary based on the mass of the parent object. This is a very important element for launching spacecraft.
Escape velocity examples:
Moon: 2.4 km/s
Earth: 11 km/s
Jupiter: 58 km/s
Sun: 600 km/s
White dwarf: 5,000 km/s
Neutron star: 76,300 km/s
Black hole: >300,000 km/s
Combining his cannonball thought experiment with his laws of motion and his law of universal gravitation, Newton was able to gain a comprehensive understanding of orbital motion.
WEIGHTLESSNESS IN ORBIT
An orbiting body is effectively in free fall and an object in free fall is weightless. This is why people on board the International Space Station are able to float around even though they are still experiencing about 90% of Earth’s gravity.
BARYCENTER
Even within a significantly asymmetrical two-body system, the larger body is never completely stationary. Take the Sun, for example. At a glance, our star appears to be the unmoving anchor for which everything else is helplessly thrown around. But even something as massive as the Sun is not invulnerable to the effects of gravity.
The barycenter is the center of mass of a two-body system, or a common point around which two objects orbit. Where the barycenter is located depends on the masses of the two objects.
If the objects are of equal mass, the barycenter will lie exactly halfway between them. If one object is more massive than the other, the barycenter will lie closer to that object. One object can be so much more massive that the barycenter lies inside the object itself. Jupiter is the only object in the solar system for which its barycenter with the Sun lies outside the Sun’s surface, even if only slightly so.
Another example in our solar system of a barycenter lying outside of orbiting bodies would be the dwarf planet, Pluto, and its largest moon, Charon. This is also common in binary star systems.
This gets much more complicated when you are dealing with three or more objects (aka the three-body problem) where the predictability of the orbits drops significantly and why the stability of our solar system is so special.
LAGRANGE POINTS
Named after the Italian-French mathematician, Joseph-Louis Lagrange, Lagrange points are regions of space around two massive objects in which the gravitational force between them reaches an equilibrium. Satellites sent to these regions are able to maintain stable orbits without experiencing a net gravitational force in any direction. This ultimately saves a lot of fuel and allows for continuous observations of Earth, the Sun or distant astronomical objects.
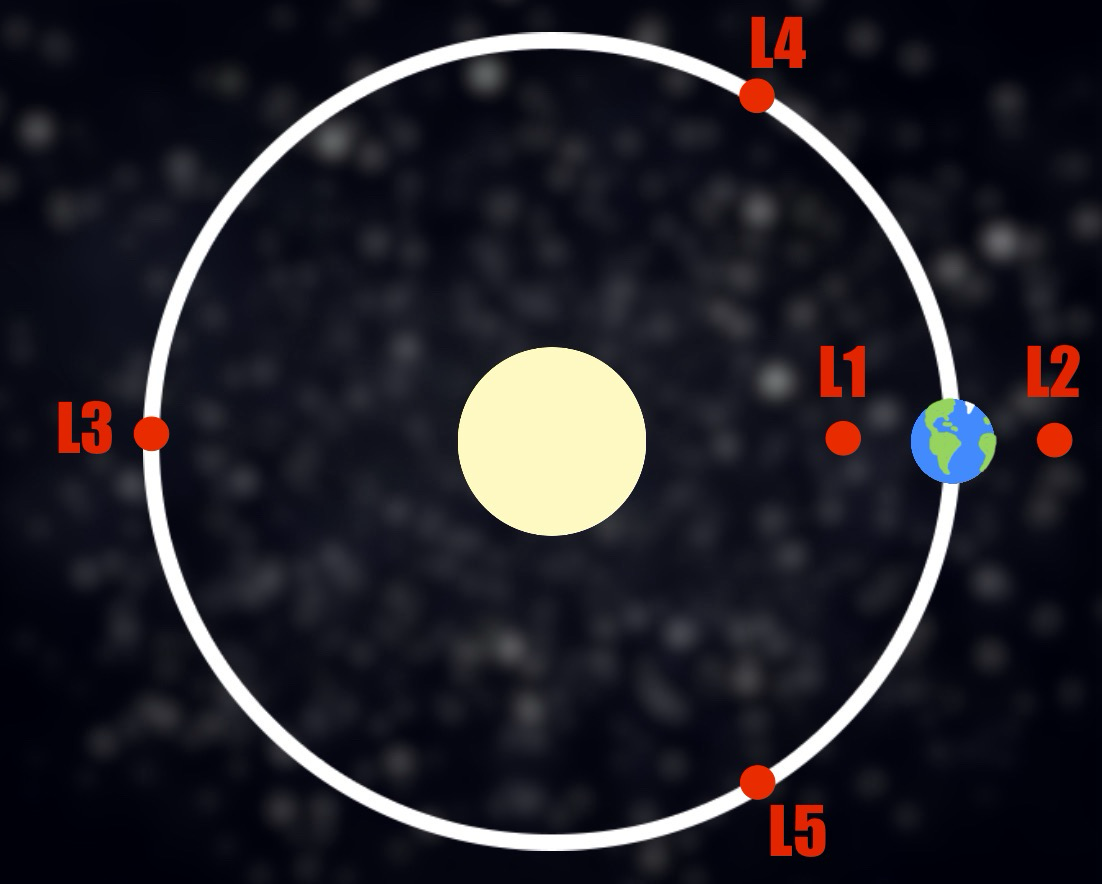
There are five Lagrange points that exist between any massive two-body system (labeled L1-L5), whether it be a planet and a moon or a star and a planet. Most relevant to humanity is the Sun-Earth system.
L1 is located between the Sun and Earth at about 1.5 million km from Earth. It is particularly useful for space telescopes to have an uninterrupted view of the Sun.
L2 is located on the far side of Earth at about 1.5 million km from Earth. It is particularly useful for space telescopes to observe deep space objects while being shielded from the brightness of the Sun and Earth.
L3 is located on the far side of the Sun at about 150 million km from the Sun and 300 million km from Earth. Scientists have yet to find a practical use for it yet.
L4 forms an equilateral triangle with the Sun and Earth, located 60° ahead of Earth’s orbit, or 150 million km. It is also known as the leading Lagrange point.
L5 forms an equilateral triangle with the Sun and Earth, located 60° behind Earth’s orbit, or 150 million km. It is also known as the trailing Lagrange point.
L1, L2 and L3 are considered positions of unstable equilibrium, meaning that any object placed there will eventually fall out of it, unless acted upon. This is why you tend not to find natural objects in these regions. L4 and L5 are considered positions of stable equilibrium and allow for the accumulation of natural objects over time. In the Sun-Jupiter system’s L4 and L5, there is a massive accumulation of asteroids called the Greek asteroids and the Trojan asteroids, respectively.
TIDAL FORCES
TIDAL FORCE
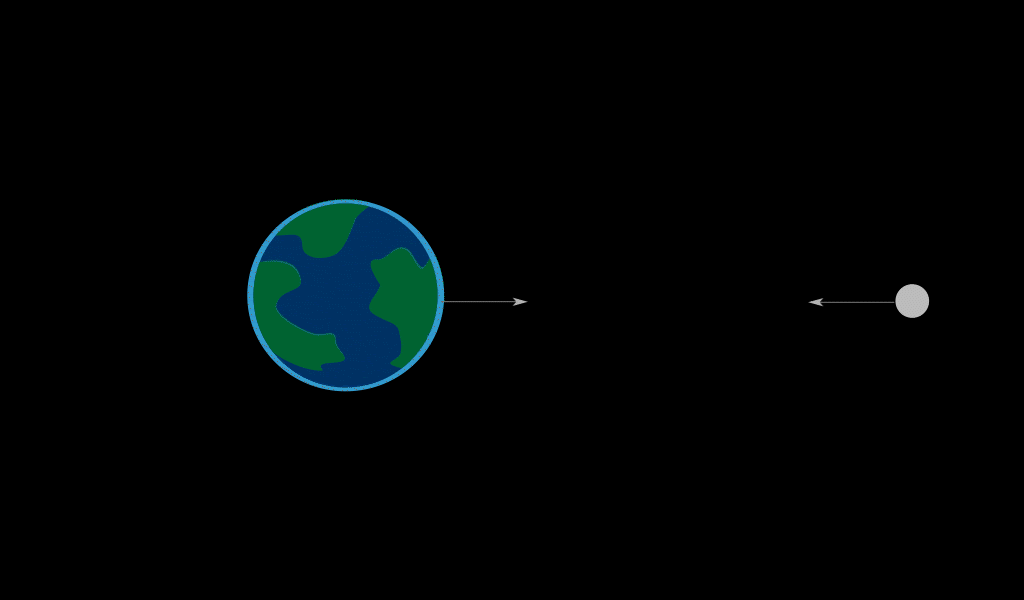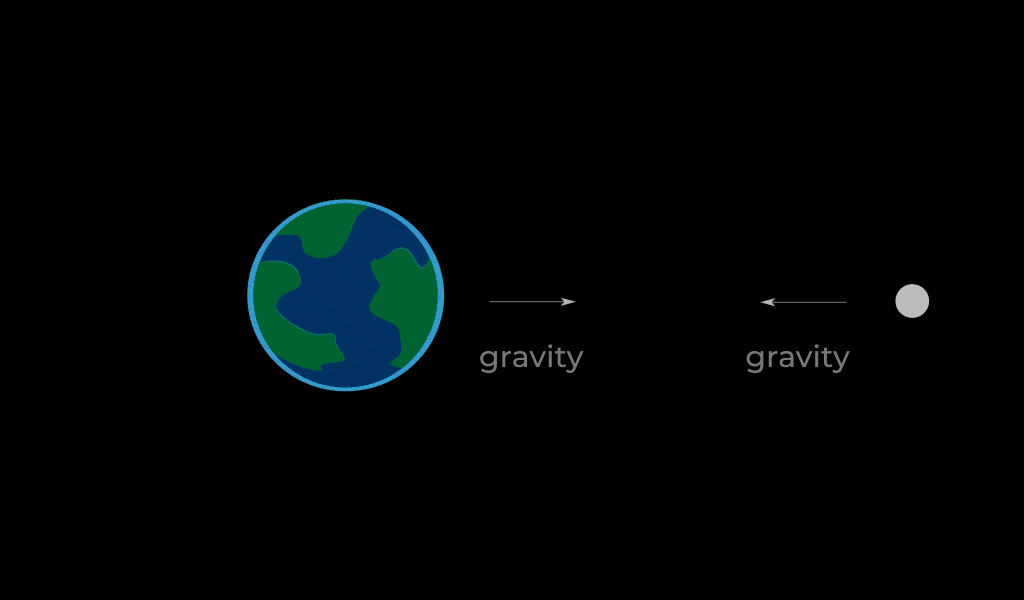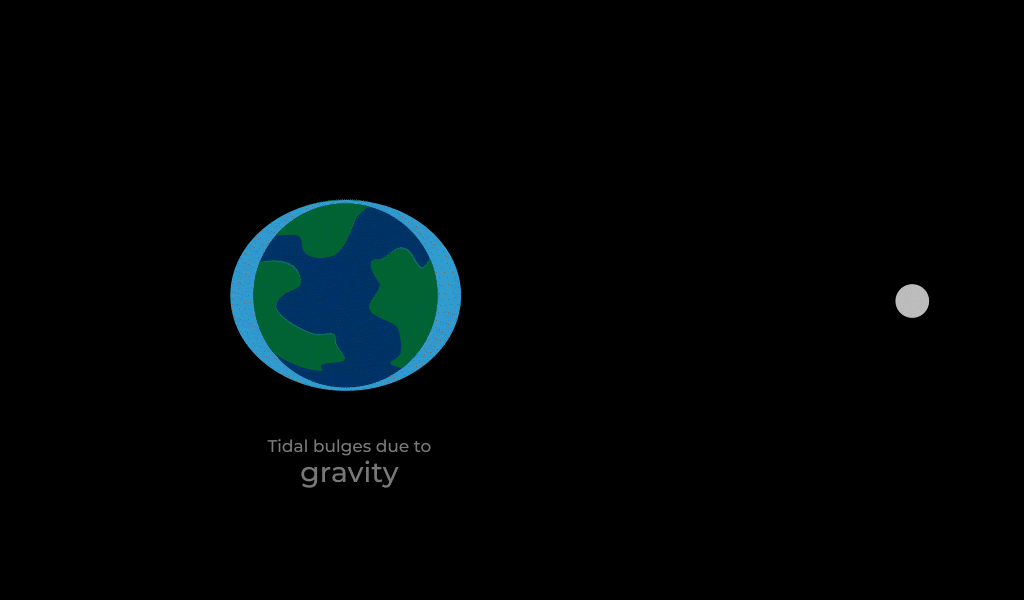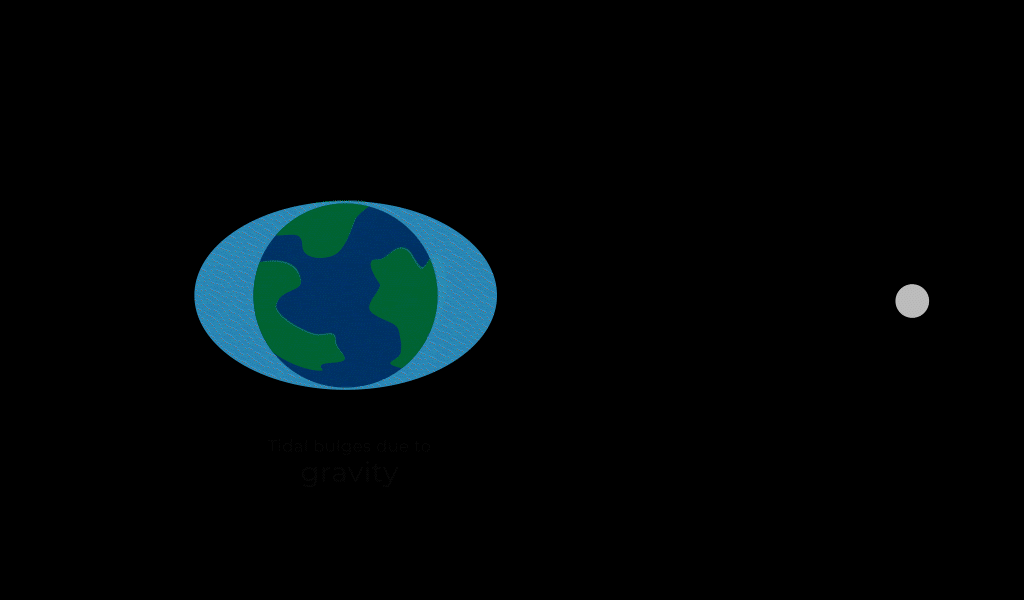
Because gravity weakens with distance, the strength of gravity that an object exerts on another will be stronger on the second object’s near side than it will be on the second object’s far side. This results in the second object being stretched. This gravitational effect is known as the tidal force. The most relevant example of tidal forces in our lives are those between the Earth and the Moon.
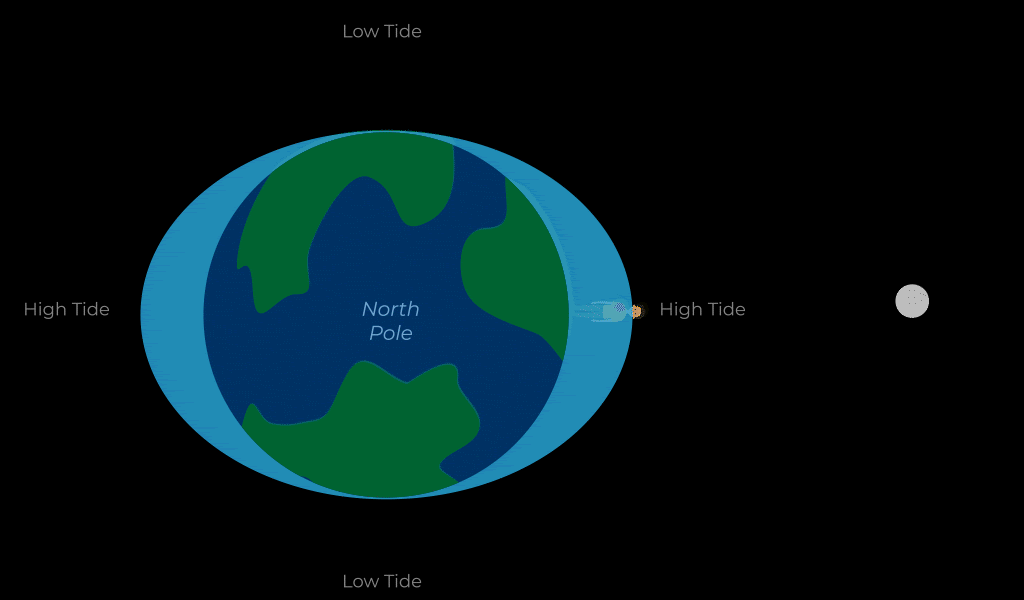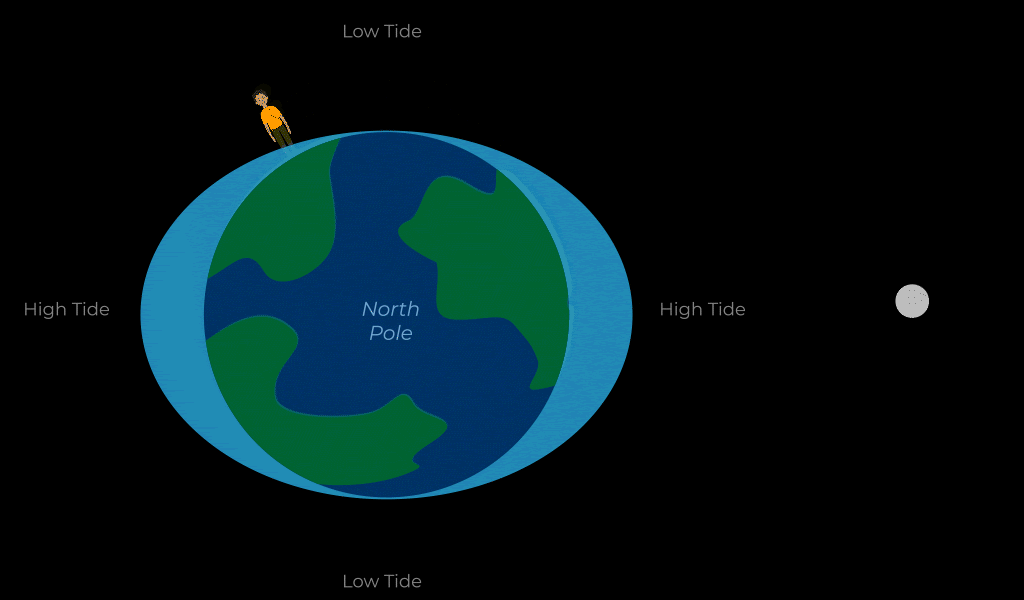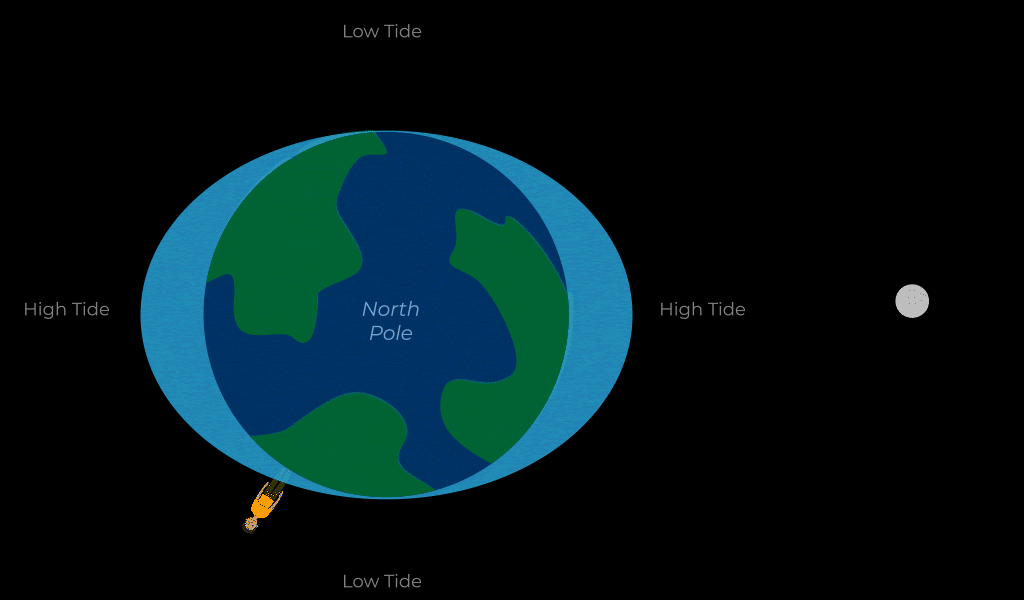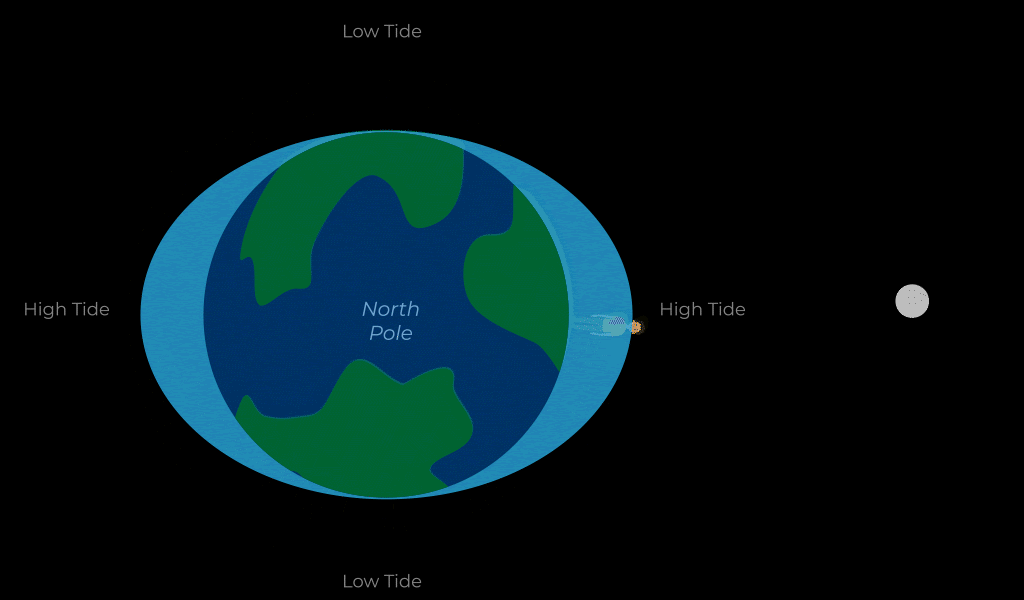
THE TIDES
As the Earth rotates, different sides of it experience tidal forces from the moon throughout the day. We experience this in the form of the tides which are the twice daily rise and fall of sea levels. That is to say that, throughout the day, you will experience a high tide where the sea levels rise, then 6.2 hours later you will experience low tide, then in another 6.2 hours you’ll experience a second high tide followed by a second low tide 6.2 hours after that.
How much the sea level rises and falls is called the tidal range, and it depends on a variety of factors including the relative positions of the Sun and Moon and the topography of the local area. The open ocean ranges 1-3 feet while coasts and bays range 6-12 feet or more.
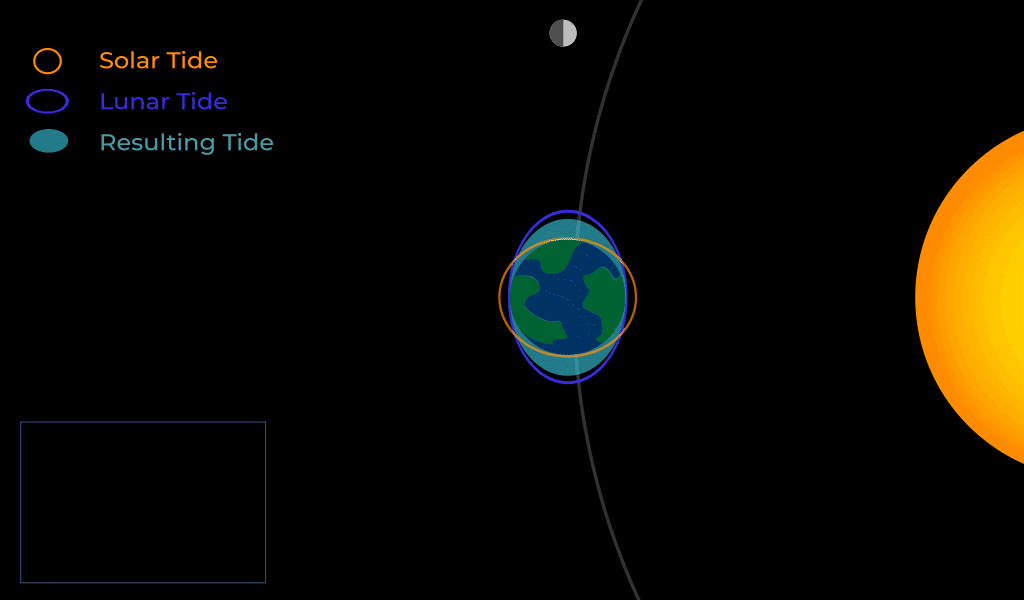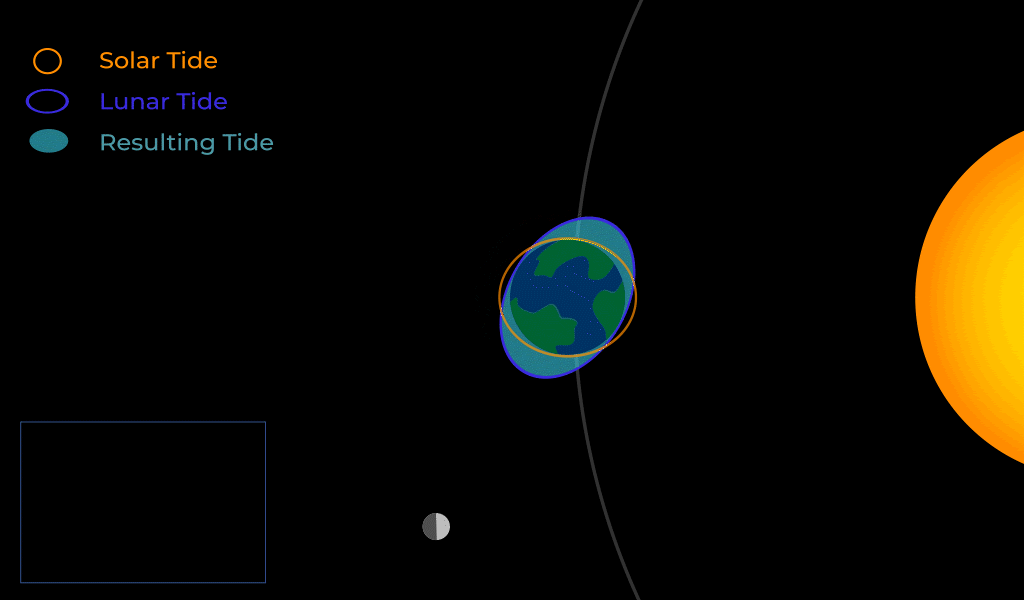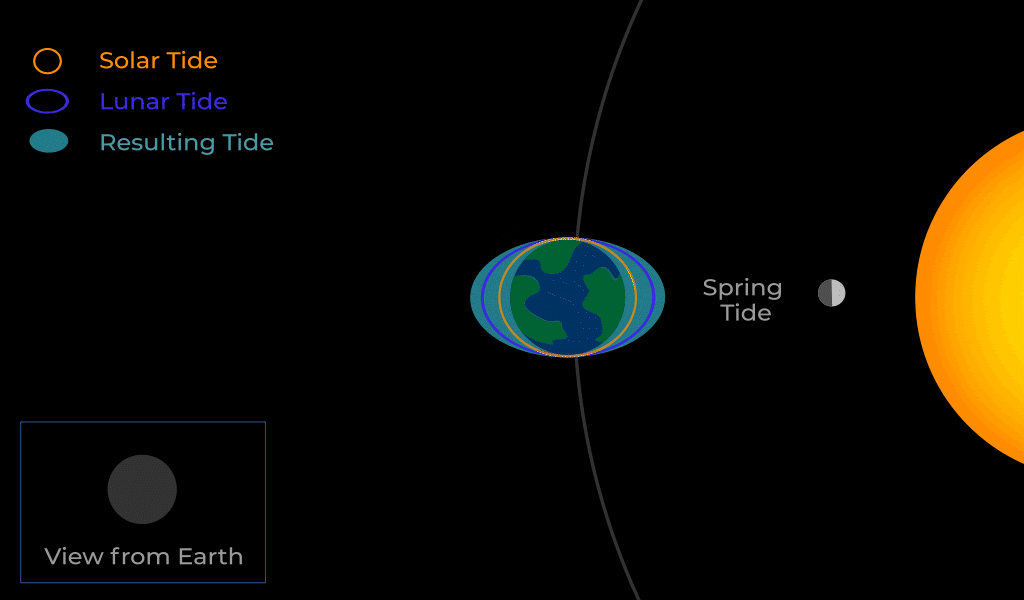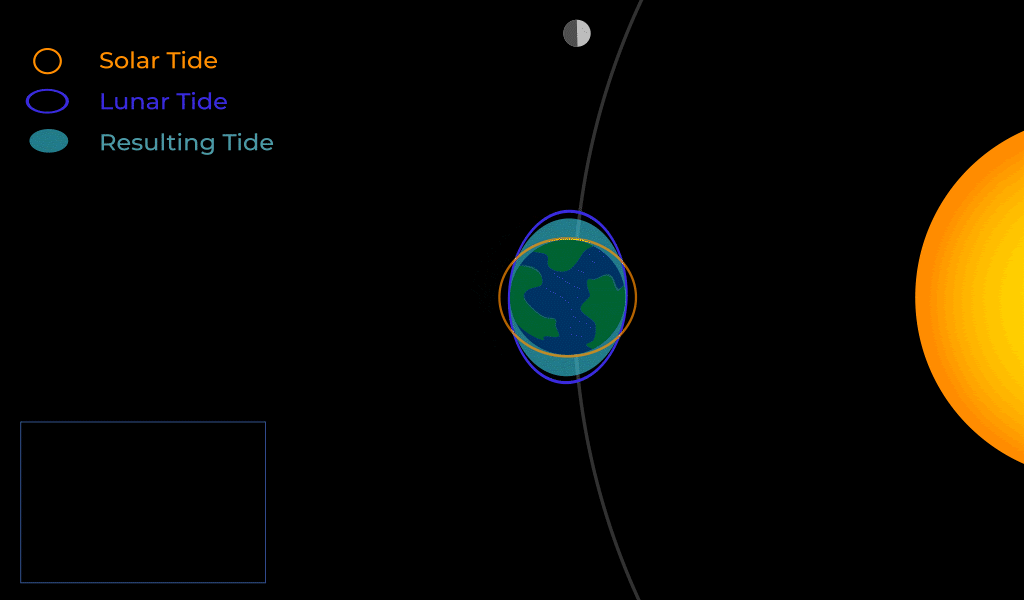
The Sun also exerts a tidal force on Earth but not as strongly because it is so distant. Throughout the month, the tidal forces of the Moon and Sun will align in various ways.
When the Moon is at the first or third quarter moon we get neap tides on Earth, where the high tides and low tides are more moderate.
When the Moon is new or full we get spring tides on Earth, where the tides are more extreme.
TIDAL LOCKING
Just as the moon creates a tidal bulge on the Earth, so too does the Earth create a tidal bulge on the moon. Also like the Earth, that tidal bulge when the moon first formed was slightly out of alignment from Earth’s position. The gravitational pull on the moon’s tidal bulge by Earth (which is much more powerful) caused the moon’s rotation to gradually slow as well. The rotation slowed until the rotation period became equal to its orbital period. This results in the same side of the moon always facing the Earth as it revolves around it. This means the moon is tidally locked.
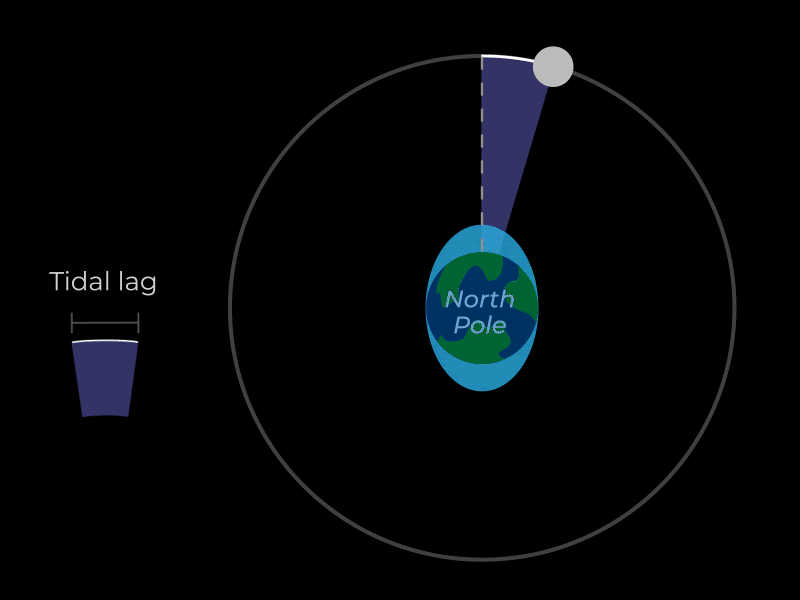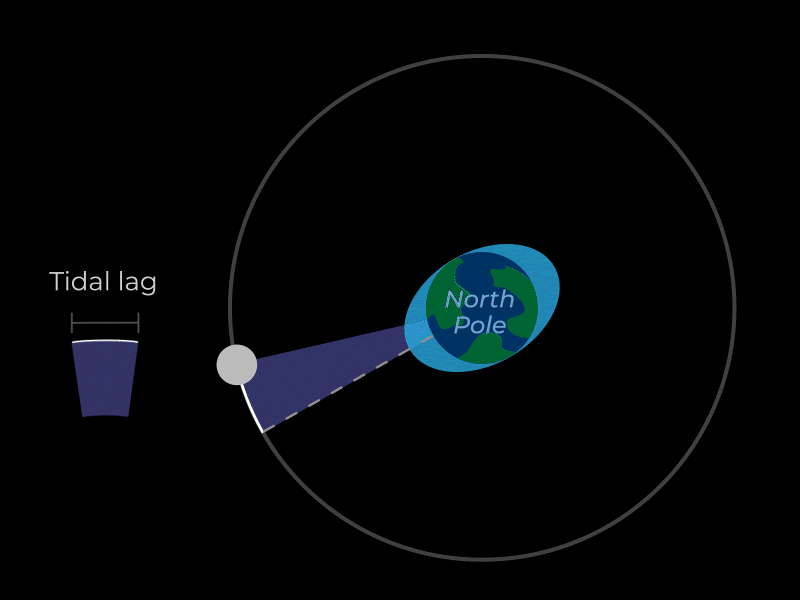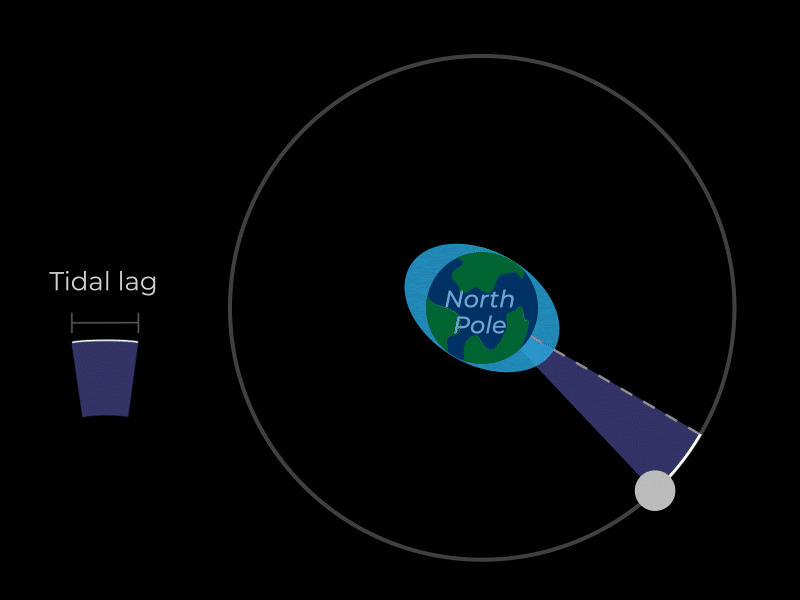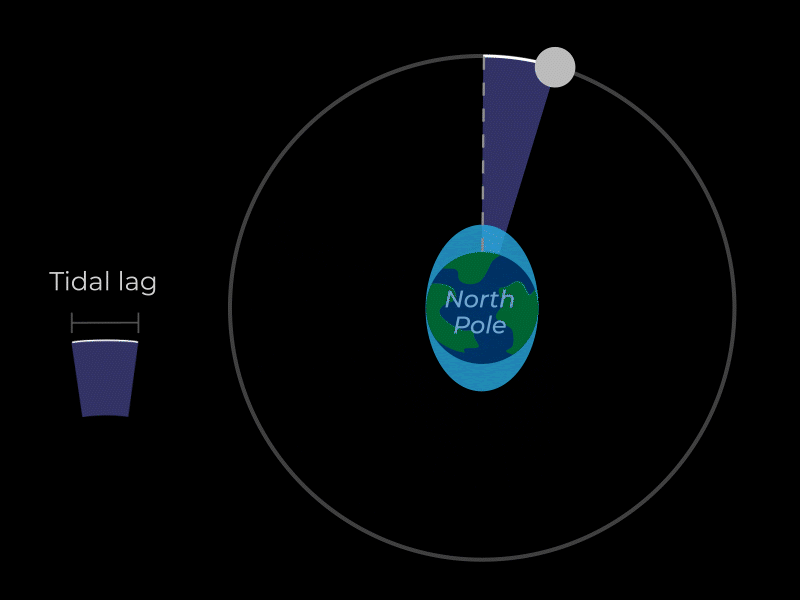
TIDAL FRICTION
Earth’s rotation carries its tidal bulge slightly ahead of the moon’s position. This creates a torque via the gravitational force between the tidal bulge and the moon. This torque causes a transfer of angular momentum from Earth’s rotation to the moon’s orbit. In other words, the Earth’s tidal bulge tugs on the moon like a dog on a leash, which causes the moon to drift into a higher orbit while the counterforce of the moon’s inertia simultaneously pulls back on the Earth’s tidal bulge, slowing the Earth’s rotation. This is called tidal friction. A day on Earth gets 1 second longer every 50,000 years and the moon into drifts away from Earth by 1.5 inches (4 cm) every year.
ROCHE LIMIT
As you approach a planet there is a region surrounding it in which the strength of its gravity begins to spike. This is where the planet’s tidal force is strongest. For small things, like a human, the tidal force is negligible. However, sufficiently large objects like moons often span dozens to thousands of kilometers. This greater difference between the near side and the far side means greater tidal forces. There is a threshold around the planet in which the tidal force trying to pull the moon apart overpowers the moon’s gravity trying to hold it together. This is called the Roche limit. As a moon approaches this boundary, it is stretched more and more until it is ripped apart into countless pieces. The resulting field of dust and debris will often continue to orbit around the planet and form into a planetary ring system, like what we see on Saturn.
It should be noted that the Roche limit is relative to the respective objects involved. It is dependent on the mass of both the planet and the moon, as well as the moon’s size. The more massive the planet, the stronger the tidal force. The larger the moon, the greater the difference in the pull of gravity between the closer side and farther side.
EINSTEIN’S THEORY OF RELATIVITY
Newtonian physics guided the scientific world for over two hundred years. Astronomers happily applied his laws of motion and law of universal gravitation to the movements of the heavens, and everything seemed to be working out. Mostly. There were certain things that Newton failed to explain and questions about the inconsistencies with the behavior of light, space and time were becoming more and more frequent. The limitations of Newtonian physics were particularly apparent in the presence of very fast-moving objects and very strong gravitational fields. This is where another visionary figure in science came in.
In 1905, German theoretical physicist Albert Einstein presented his special theory of relativity. It postulated the following things:
The speed of light is constant regardless of the motion of the light source or the observer.
Time is relative, depending on the relative motion between the observer and the observed.
The length of an object appears to contract when it’s in motion relative to the observer.
Energy and mass are interchangeable where a small amount of mass can be transformed into a large amount of energy or vice versa.
The idea of relativity did not originate with Einstein. Descartes, Kepler and Galileo had pondered relativistic ideas in the early-17th century but it was Einstein that implemented this idea into applicable mathematical frameworks. All of these are profound and complex ideas in their own right but let’s talk about just one of these in particular: “Time is relative.”
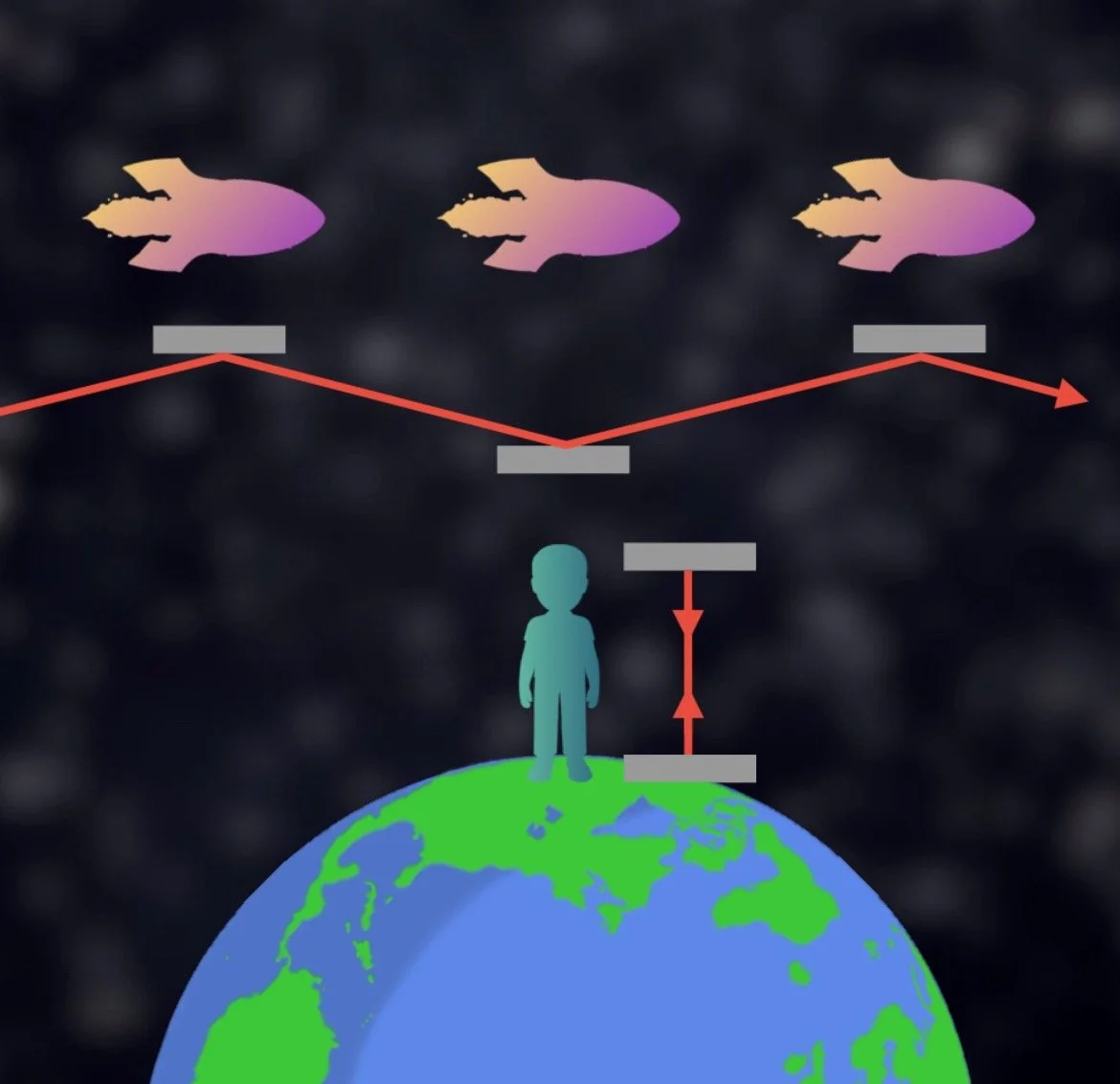
Imagine a person is standing on Earth and another person is standing inside of a spaceship passing over Earth. Also inside the spaceship is a laser being bounced up and down between two mirrors. From the perspective of the person on the spaceship, that laser is simply moving up and down. From the perspective of the person on Earth, that laser is not only moving up and down but also moving sideways inside the passing spaceship. That means that the laser is simultaneously moving two different distances in the same amount of time. How is this possible? Time is passing at different rates for both people. Specifically, the person in the moving spaceship is experiencing time slower than the person on Earth. This relativistic effect is called time dilation.
So, what does this all have to do with gravity?
Well, Einstein was not finished with relativity in 1905. His theory only applied specifically to objects that are in relative but constant motion, hence why it is called “special” relativity. Einstein continued to expand and broaden this idea and ten years later, in 1915, he presented his general theory of relativity. So, what does it say?
What we think of as empty space is actually four-dimensional spacetime, a sort of “fabric” that fills the volume of the universe. Gravity is not to be thought of as a force but rather the curvature of spacetime caused by the presence of mass and energy. This may sound a bit out there at first but stick with me.
Let’s visualize spacetime as a two-dimensional plane of stretched, elastic fabric. Let’s use the jumping mat of a trampoline as a representation. In this way, spacetime is said not to be absolute or fixed, but quite malleable under significant enough applied forces. When nothing is placed on the trampoline, the fabric remains unchanged. Let’s imagine a heavy bowling ball is placed at the center. The weight of the bowling ball sinks into the fabric and forms a depression. If the fabric represents spacetime then the weight of the bowling ball represents its force of gravity. ‘The heavier the object, the deeper it sinks’ translates to ‘the more gravity an object has, the more it warps spacetime.’
Next, imagine we start rolling a bunch of smaller billiard balls and marbles across the fabric. What happens? They start to follow the circular curvature of the depression of the fabric created by the bowling ball’s weight. They actually start to mimic the orbit of moons around planets and planets around stars.
This concept is succinctly summarized by the physicist John Archibald Wheeler: “Matter tells spacetime how to curve, and curved spacetime tells matter how to move.”
There is a really cool video of a physics professor actually demonstrating this exact thing.
You can see it here: Gravity Visualized - YouTube
Keep in mind that this idea of spacetime as a two-dimensional fabric is merely a simplistic analogy. In actuality, spacetime occupies four dimensions (that’s three spatial dimensions and one time dimension). Remember that it isn’t just space that is warped by gravity, but spacetime. Just like with the time dilation caused by the speed of an object in Einstein’s special relativity, so too is it caused by the gravity of an object. In this case, the higher the gravity, the slower the passage of time. The lower the gravity, the faster the passage of time. This may sound like science fiction, but engineers actually do have to adjust the clocks on satellites to account for the effects of time dilation because they travel at very fast speeds high above Earth’s surface where gravity is weaker. This causes their clocks to run very slightly slower, but the discrepancy accumulates over time.
If things aren’t already strange enough, let’s really dive deep into the extreme. Quite literally for this next part. What would happen if we placed an infinitely heavy object on the trampoline? Presumably the object would create an infinitely deep depression. Are there any objects in the universe analogous to this?
BLACK HOLES, SINGULARITIES & RIPPLES IN SPACETIME
Black holes are extremely dense objects with such terrifyingly strong gravity that not even light can escape. The boundary at which this point of no return occurs is called the event horizon. Within this region is nothing but blackness. A dark void of extremes where things go in and never come out. The actual object producing this gravity is hidden somewhere within the heart of that abyss that devours all that strays too close. For this reason, we never actually observe a black hole directly. We can only observe the effects it has on its surroundings. Plus, it’s always a little suspicious when we see stars seeming to orbit around nothing.
A common myth is that black holes are just giant space vacuums that suck in everything indiscriminately. As extreme as black holes are, the areas surrounding them still operate on the classic principles of gravity. If we suddenly replaced our Sun with a black hole of equal mass, Earth would still continue to orbit that object as if nothing had changed (other than it becoming very dark and cold).
One of the most significant effects we associate with black holes happens beyond the event horizon. In this surrounding region, the warping of spacetime bends, distorts and magnifies any light happening to pass through its vicinity. This phenomenon is called gravitational lensing.
From our vantage point on Earth, we see light that comes from a faraway galaxy which moves towards us in a straight line. But what if a black hole were positioned between us and that distant galaxy? The light on its way to us would be intercepted by the black hole’s strong gravitational field and be bent around the object. Depending on a number of factors, the light could be bent in different ways. It could simply curve around the object, appearing as a distorted shape at the edge of the gravitational field. It could be split into multiple images that appear on different sides of the void. It could form a complete ring of light around the black hole (called an Einstein ring). The gravity could even focus and magnify the light, making the background galaxy appear brighter than it otherwise would be.
Based on these effects, we can actually learn important information about both the background object and the object causing the gravitational lensing. It also allows us to see objects that are otherwise too far and dim to see.
Gravitational lensing isn’t just produced by black holes, either. Entire galaxy clusters can have enough combined gravity to create similar effects. The lensing effect is often much more complex as galaxy clusters are not merely one object but many producing the effect. Even some individual galaxies and stars can be massive enough to produce some gravitational lensing effects. This image was taken by the James Webb Space Telescope showing a massive galaxy cluster distorting background galaxies and making them appear as streaks of light.
Another strange way gravity warps spacetime comes in the form of gravitational waves. These are ripples in spacetime generated by the acceleration of massive objects. The waves propagate outward from the source in all directions and at the speed of light, stretching and squeezing spacetime. All gravitational systems can create gravitational waves, but they are usually so weak that Einstein himself didn’t expect they would ever be detectable. However, advanced observatories like the Laser Interferometer Gravitational-Wave Observatory (LIGO) have been detecting them directly since 2015. They are generated by some of the most powerful and violent events in the known universe. Sources include fast-spinning neutron stars, the explosion of high-mass stars called supernovae, and most dramatically, the collision of neutron stars or black holes. These gravitational waves carry with them vital information about their origins. For example, the frequency of the waves tells us the masses of the objects and the strength of the waves tell us how far away the event happened.
Note: It is suspected that the big bang itself generated gravitational waves that still propagate through the universe.
Because black holes have such extreme gravity, they also have extreme tidal forces. Let’s imagine a person falling feet first toward a black hole. The gravity pulling at the person’s feet would be much stronger than the gravity pulling at their head. This would no doubt stretch the person more and more as they fell further and further. In fact, the gravity difference would be so dramatic that the person would theoretically be stretched out into a long, thin strand of matter. This phenomenon is lovingly referred to by scientists as “spaghettification.” Yeah, really.
An object falling into a black hole will eventually reach the center, an infinitely small, infinitely dense point known as the singularity. Spacetime as we know it would curve into infinity and the object that reaches this point would essentially cease to exist in any meaningful way.
Because the singularity is hidden deep within the event horizon, we don’t have the means to observe or study this region. We only have what the math says should happen and that’s the problem. Within a singularity, the laws of physics as we understand them seem to break down and even relativity can no longer account for what happens there. This mystery also holds for questions about the Big Bang as scientists highly suspect the universe as we currently know it began in a singularity-like state.
That’s not to say that Einstein’s relativity ceases to apply in all the ways that came before, just as relativity itself did not render Newton’s classical mechanics null and void. They simply work at different scales of extremity. We have reached another plateau to climb, and scientists are at the frontier working to figure it out. The field of quantum mechanics seems to be the next most promising iteration but, for now, we’ll have to wait and see. Maybe someone is out there right now, either actively working as a scientist or just starting their journey for knowledge at this very moment, and they may lead us to the ultimate answer, or at least the next great leap forward.
Gravity is beautifully simple and complex all at the same time.
If you or anyone you know are looking to learn more, members of the Harford County Astronomical Society are here for you to provide our enthusiastic knowledge and experience.
Come find us at future events or fill out an outreach request form and ask for assistance and we will do what we can!